What's different about a Matryoshka SAE?

This project has an interesting history. The authors are Nabeshima, Bussman, Leask and Nanda; Noa Nabeshima published on LessWrong about it on Dec 13, 2024 and the other three published their own post six days later, on Dec 19; apparently the two groups had been working in parallel, and even used the same name for the technique (matryoshka SAEs) independently. Then they ended up writing a paper about it together! Nice to see that they merged their projects :)

Here's how a Matryoshka SAE is different from a regular SAE. You start by creating a list of numbers $\mathcal{M}=m_1, m_2, ...,m_n$ with $m_1 < m_2 <... < m_n$. Each $m_i$ corresponds to an SAE which must use only $m_i$ latents to reconstruct the inputs.

We encode the SAE with $$f(x) = \sigma(W^{\text{enc}}x + b)$$ where $\sigma$ is an activation function, in this paper BatchTopK. BatchTopK zeros everything but the activations that are largest after encoding the whole batch. (See the paper for more details.) Then for each each SAE (indexed by $i$) we have $$\hat{x}_i(f) = W^{\text{dec}}_{0:m_i, :}f_{0:m_i}+b^{\text{dec}}$$ with this notation indicating we're taking the first 0 to $m_i$ rows of matrix $W$ and multiplying on the left with the first 0 to $m_i$ indices of the encoded latent vector $f$. See footnote ¹ if you are confused about the weight-indexing notation, because I am too.

For example: $\mathcal{M} = 1,5,20$: you encode the vector into the residual stream, and then you have 3 sub-SAEs. The sub-SAEs must use only the first $m_i$ elements of the latent vector and only $m_i$ corresponding rows (again see footnote¹ but notation doesn't matter that much) of the decoder weights matrix.

Thus when we decode, we have 1 SAE using a top-1 decoding, one SAE using a top-5 decoding, and 1 SAE using a top-20 decoding. Then we use a specialized loss function to evaluate this. "The key innovation in Matryoshka SAEs is the training objective that enforces good reconstruction at multiple scales simultaneously." That loss function as provided in the paper is $$\mathcal{L}(x) = \sum_{m \in \mathcal{M}} ||x-(f(x)_{0:m} W^\text{dec}_{0:m} + b^{\text{dec}})||^2_2 +\alpha\mathcal{L}_{\text{aux}}$$ with two parts. The first part is typical MSE loss between $x$ and $\hat{x}$ , summed over each element. The second is the auxiliary loss we get from Gao et al 2024:

We find two important ingredients for preventing dead latents: we initialize the encoder to the transpose of the decoder, and we use an auxiliary loss that models reconstruction error using the top-$k_{\text{aux}}$ dead latents (see Section A.2 for more details).

...

(from Section A.2) We define an auxiliary loss (AuxK) similar to “ghost grads” Jermyn and Templeton, 2024 that models the reconstruction error using the top-$k_{\text{aux}}$ dead latents.

The auxiliary loss incentivizes dead neurons to come alive again by giving a "dead neuron penalty." Then you train this the normal way with gradient descent. You can probably find more details in Bart Bussman's or Noa Nabeshima's GitHub pages; they both published code :)

In summary, there are multiple sub-SAEs which are sharing the same weights. Each sub-SAE is only allowed to use a subset of those weights to decode a shared encoded vector which will always contain the elements of the smaller SAEs' subsets. The theory here is that it incentivizes the latents used by the smallest sub-SAE to include high-level, broad features, while the weights used by larger SAEs can be more precise. Problems we were previously concerned about like feature splitting can be meaningfully (but not totally) alleviated. Here's a diagram:

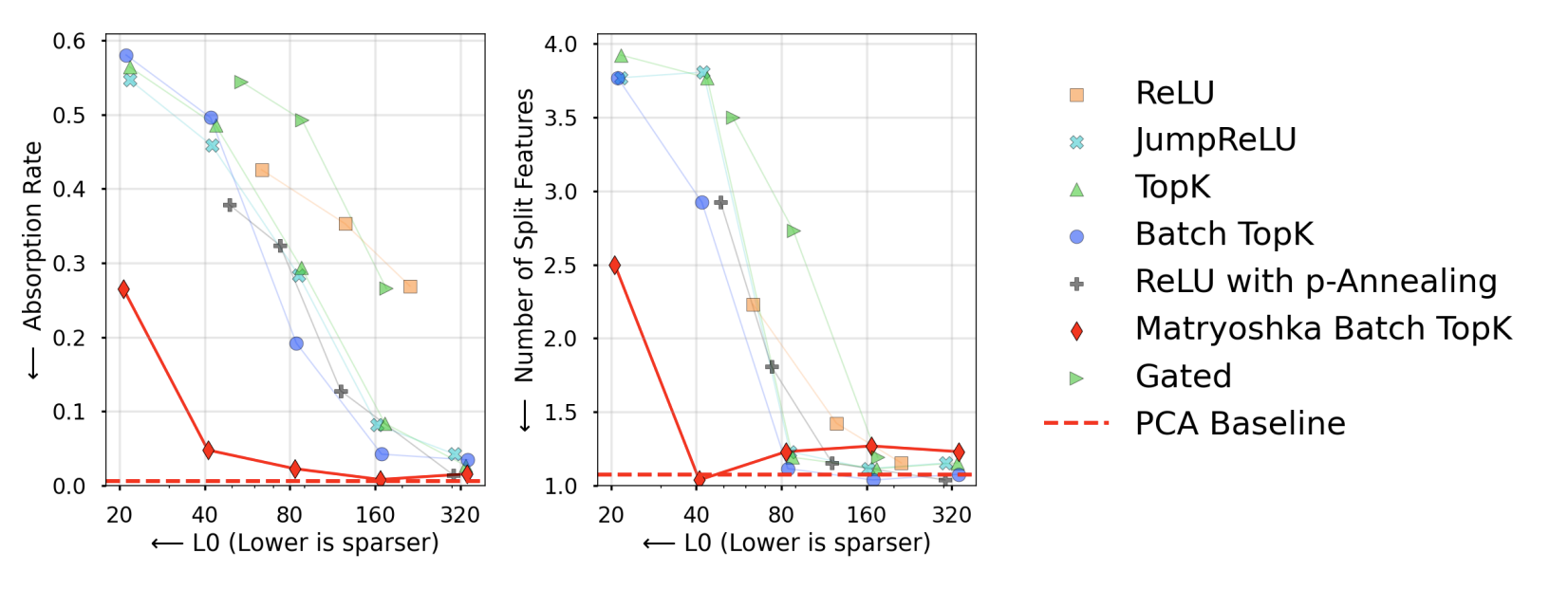
I'm not sure what it means that they got below the PCA baseline — my guess is that it means that their raw number of split features is lower for the Matryoshka SAE than it is for the first 40 principal components when you do PCA? This is interesting. They never discuss it in the paper. I'd like to do a future blog post on PCA.

Footnotes