Four Papers: Align and Translate, Seq2Seq, Pointer Networks, and Attention

(This diagram required extensive staring-at to understand, but it looks kinda pretty so I'm using it as the post thumbnail. This is from the Pointer Networks paper, see below for link.)

Neural Machine Translation by Jointly Learning to Align and Translate (2014)

(Link)

This paper introduces the attention mechanism, though described in a different terminology, and with some extra fun features.

Problem: The general idea that is proposed is that RNNs are bottlenecked: previous work had just used an encoder-decoder RNN model for translation, where you encode the entire sentence into a fixed-size "context" vector using an RNN, then use that as your initial hidden state for a decoder that outputs the translation word-by-word. This sucks because for long sentences you can't compress all the information into your fixed-size vector.

Solution: allow tokens to 'attend' to the entire input and extract information differently per-token rather than having a single context vector.

This paper's approach:

• Create "annotations" for each input state. The annotations are two concatenated vectors, one from an RNN going forward, and one from an RNN going backward.
• Compute the "energy" for each token with each annotation
• Softmax along the token dimension
• Weighted sum
• Include this context vector computation in your RNN hidden state for the next time step

Note that when you see "soft alignment" it is aligning "softly", i.e. not exactly one-to-one; hard alignment is one-to-one mapping.

That's basically the paper. A bonus thing that I got from the paper-reading club is that there are signal-processing analogies to neural networks that provide "good intuition for why people choose these architectures." CNNs can be seen as analogous to finite impulse response filters; RNNs can be seen as analogous to infinite impulse response. (I didn't really look into this, but I'm leaving it here for future consideration.)

"How do you get this from RNNs and an intro to data structures class?" Attention is basically a hash map that you altered to make learnable. (I've been told that this is a very common way of solving ML problems: "design a program that you think would solve the problem to give your model a good inductive bias, then make it learnable.") Not something I'm familiar with because I haven't taken an introduction to data structures class, lol.

Interesting notes:

• Canadian Parliament had a big role in assembling machine translation datasets; they have two official languages, yielding high-quality dual-language corpuses for English-French translation
• https://huggingface.com/papers

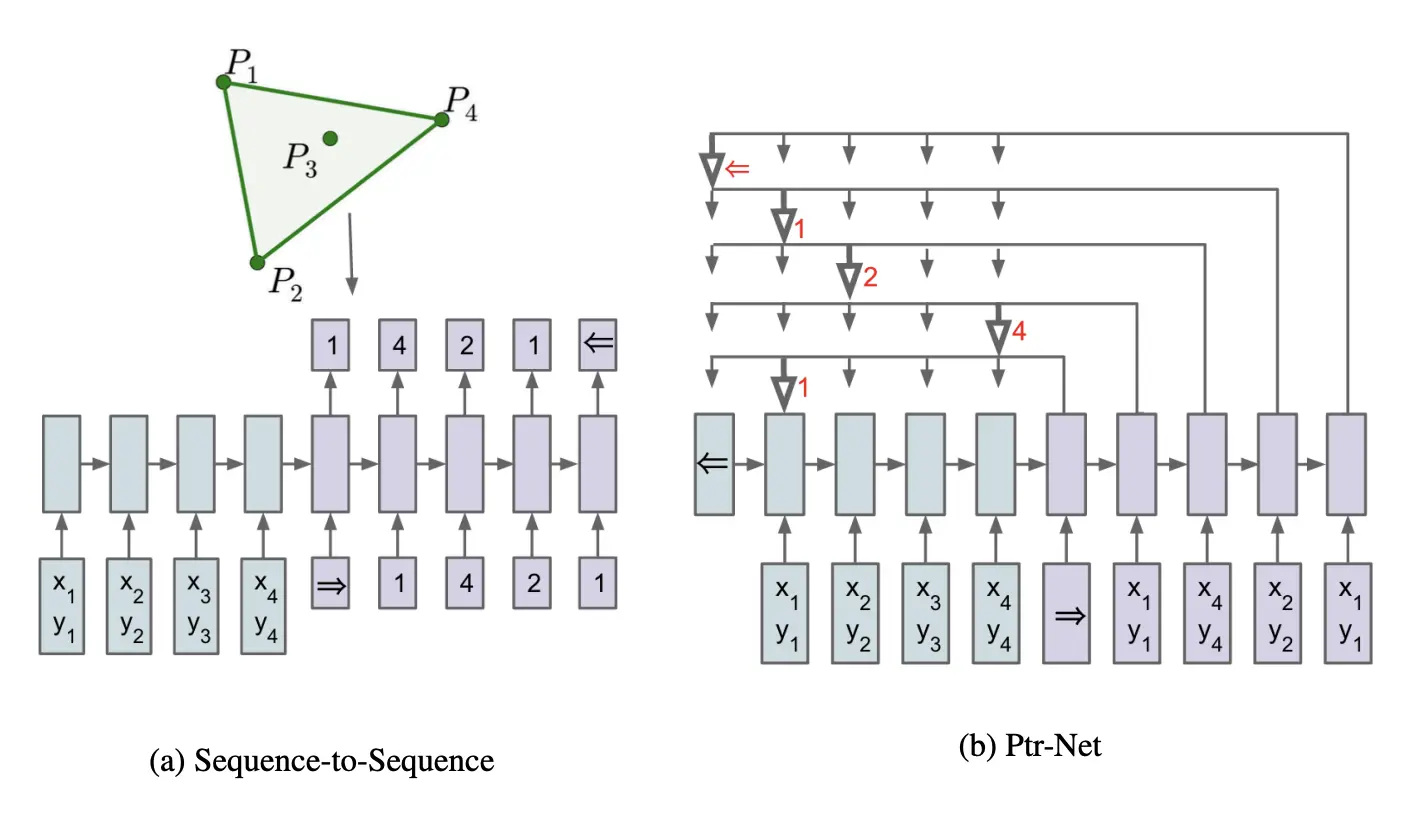
Pointer Networks (2014)

(Link)

Problem: If you want to train an RNN to output permutations or lists of indices of $n$ inputs, you have to train it to handle $n$ classes. If you want your network to output the list [1,5,6,9,1], for example, where each of those are indices of points, you would need to train the RNN to output numbers up to 9. We want an approach that scales to arbitrary $n$.

Solution: using attention, allow your RNN to simply "point" to an input, then use that original point as the input to the next layer. What you do is, as opposed to taking the attention scores and then computing a weighted sum, you take the softmaxed attention scores for each input and just consider those to be your probabilities. Take the argmax and feed the corresponding point into the next layer.

Result: It turns out that you can use this to very efficiently "solve" the traveling salesman problem, as well as other combinatorial optimization problems! I find this fascinating -- yes, *RNN-like networks can indeed learn approximate (very good approximate) solutions to computationally difficult problems like this one!

Order Matters (2016)

(Link)

(Did not really read this one, and thus did not understand it.)

Key question: How do we adapt seq2seq models to work with sets, i.e. unordered inputs?

Architecture: take your inputs in any order, feed them into an LSTM with no inputs and no outputs and run it on itself for some amount of timesteps, then token-by-token produce the output? Something like, "reorder the inputs however is optimal" (???)

Interesting facts:

• Sutskever's team reversed inputs for translation and got better results; this is an example of how order does indeed matter for performance in naive RNNs
• This is an interesting example of synthetic data!
• Most of these papers use "beam search"

Attention is All You Need (2017)

(Link)

This is the paper that everyone ever has cited all the time. I would explain this here but I think that would deserve its own post. I'll summarize multihead self-attention here just for the sake of having something here. (I explained this part to the club, so hopefully I know something about it lol)

MHSA:

1. Project $X$ (N, D) to $K$, $Q$, $V$ matrices (N, D/H) using $W_K$, $W_Q$, $W_V$ (D, D/H)
2. Compute "dot-product similarity" of each key with each query using $QK^T$ (N,N) (transpose to make dimensions match up) and normalize by $\sqrt{d_k}$ to compensate for large dot products. (Intuition: a 1000-dimensional dot product will be much larger than a 10-dimensional dot product. Divide by $\sqrt{d_k}$ to reduce variance to 1, since variance is quadratic.)
3. Softmax along the token dimension, giving intuitively your "attention scores": vector $m$ gives you how relevant every token is to token $m$.
4. "Extract amounts of information" from the V matrix, amounts of information corresponding to the attention weight
5. Concat the heads together, each (N, D/H) to get (N, D), and project this via $W_O$ (D,D) to get your MHSA output.